Решение уравнений
В данном задании необходимо решить уравнение степени больше двух — это может быть биквадратное или кубическое уравнение. Ниже мы приводим алгоритмы решения типовых заданий!
Разбор типовых вариантов задания №21 ОГЭ по математике
Демонстрационный вариант ОГЭ 2019
Решите уравнение
x4 = (4x — 5)2
Алгоритм решения:
- Определить тип уравнения.
- Перенести правую часть уравнения в левую.
- Привести уравнение к виду, при котором можно его многочлен слева разложить на множители.
- Разложить на множители.
- Приравнять каждый множитель к нулю
- Решить полученные уравнения.
- Записать ответ.
Решение:
1. Уравнение четвертой степени.
2. Перенесем правую часть уравнения в левую:
x4 — (4x — 5)2 = 0
3. Уравнение уже приведено к виду, при котором можно его левую часть разложить на множители.
4. Данное уравнение разложим на множители по формуле разности квадратов. Получим:
(х2 – (4х-5))( х2 + (4х-5)) = 0, или (х2 – 4х+5)(х2 + 4х-5) = 0.
5. Приравняем каждый множитель к нулю:
х2 – 4х+5 = 0 и х2 + 4х-5 = 0
6. Решим каждое из уравнений по формулам дискриминанта и корней:
Для первого уравнения:
D = b2-4ac = 16-20 = — 4, это означает, что первое уравнение х2 – 4х+5 = 0 не имеет корней.
Для второго уравнения:
Определим корни второго уравнения:
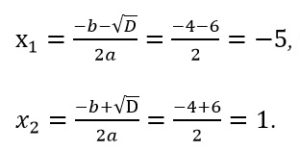Получили два корня: -5; 1.
Ответ: -5; 1.
Первый вариант задания
Решите уравнение
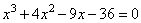
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
Решение:
1. Перед нами уравнение третьей степени общего типа.
2. Найдем делители свободного члена данного уравнения. Это числа: 1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 12; -12;.18; -18; 36; -36.
3. Рассмотрим числа 1; -1; 2; -2; 3; -3. Это наименьшие среди найденных делителей. Подставим их по очереди в уравнение вместо х:
- для x=1:
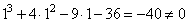— не подходит; - для x=-1:
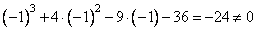— не подходит; - для х=2: 23+4∙22-9∙2=8=16-18-36=-38≠0 — не подходит;
- для х=-2: (-2)3+4∙(-2)2-9∙(-2)-36=-8+16+18-36=-10≠0 – не подходит;
- для x=3:
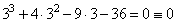— подходит.
Мы нашли один корень.
4. Теперь выполним деление кубического многочлена на x-3, воспользовавшись схемой Горнера, имеем:
| 1 | 4 | -9 | -36 | |
| 3 | 1 | 7 | 12 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
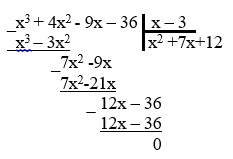
5. После деления получаем квадратный трехчлен:
x2 +7x+12.
Составим квадратное уравнение для вычисления оставшихся двух корней:
x2 +7x+12=0
6. Решим его с помощью формул корней и дискриминанта
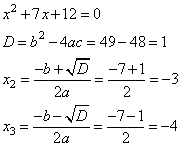
7. Получили три корня 3; -3; -4.
Ответ: 3;-3;-4.
Второй вариант задания
Решите уравнение
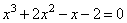
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
— для x=1: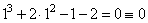 
— подходит это и есть один из корней.
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
| 1 | 2 | -1 | -2 | |
| 1 | 1 | 3 | 2 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
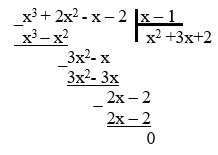
5. Получаем квадратный трехчлен
x2 +3x+2.
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
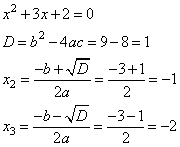
7. Получили три корня -2; -1; 1.
Ответ: -2; -1; 1.
Третий вариант задания
Решите уравнение
(х–2)4+3(х–2)2–10=0.
Алгоритм решения:
- Выполняем замену выражения с х на альтернативную переменную. Это позволит упростить уравнение и привести его к форме обычного квадратного.
- Решаем полученное квадратное уравнения.
- Переходим обратно к выражению с х, для которого была выполнена замена.
- Находим искомые корни уравнения.
Решение:
(х–2)4+3(х–2)2–10=0
Выполняем замену: (х–2)2=а.
Получаем:
а2+3а–10=0
Это уравнение можно решить с помощью т.Виета. Согласно теореме, имеем:
а1+а2=–b, a1·a2=c.
Здесь а1, а2 – корни этого уравнения, b=3, c=–10.
Отсюда получаем: а1=2, а2=–5.
Возвращаемся к переменной х. Поскольку (х–2)2=а, то получим:
1) (х–2)2=2
2) (х–2)2=–5
это уравнение корней не имеет, т.к. нельзя извлечь корень из отрицат.числа
Ответ: 
Четвертый вариант задания
Решите неравенство
(3х–7)2≥(7х–3)2.
Алгоритм решения:
- Используя ф-лу сокращенного умножения для квадрата разности, раскрываем скобки в левой и правой части нер-ва.
- Группируем элементы (слагаемые) неравенства: слагаемые с «х» должны оказаться в левой части, свободные члены – в правой. Приводим подобные.
- Решаем полученное нер-во.
Решение:
9х2–42х+49≥49х2–42х+9
9х2–42х–49х2+42х≥9–49
–40х2≥–40
х2≤1
х≤|1| → –1≤x≤1 → xϵ[–1; 1]
Ответ: [–1; 1]
Пятый вариант задания
Решите систему уравнений
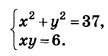
Алгоритм решения:
- Из 2-го уравнения выражаем у через х.
- Подставляем полученное выражение для у в 1-е уравнение.
- В полученном ур-нии с одной переменной (х) выполняем тождественные преобразования. Приводим его к квадратичному виду.
- Выполняем замену х2 на а. Решаем полученное квадратное ур-ние.
- Возвращаемся от а к х. Находим все значения (корни) для х.
- Определяем соответствующие им значения для у.
- Фиксируем в ответе пары соответствующих корней.
Решение:
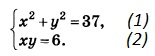
Из (2) выражаем у через х:
Полученное выражение для у подставляем в (1):
Выполним преобразования:
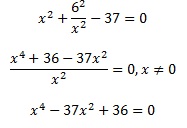
Выполним замену: х2= , а≠0 .
Получим:
а2–37а+36=0
По т.Виета а1=1, а2=36
Отсюда имеем:
х2=1 → х=±1 → х1=–1, х2=1
х2=36 → х=±6 → х3=–6, х4=6
Теперь возвращаемся к уравнению, в котором у выражено через х. И вычисляем соответствующие значения для у:
Ответ: (–1; –6), (1; 6), (–6; –1), (6; 1)
