Задание №14 ЕГЭ по математике профильного уровня

Стереометрия

---

Задание №14 — стереометрия в профильном ЕГЭ по математике. В задачах данного уровня необходимо проявить знания как по планиметрии, так и по стереометрии. Однако многие задания опираются на теорему Пифагора, поэтому опыт решения аналогичных задач будет только плюсом. Перейдем к рассмотрению одного из таких заданий.

---

Разбор типовых вариантов заданий №14 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

Алгоритм решения:

а)

1. Выполняем чертеж, соответствующий условию и проводим высоту ВН.
2. Вычисляем длину высоты ВН.
3. Вычисляем BN.
4. Показываем, что BM и MN перпендикулярны.

б)

1. Проводим перпендикуляр NP к ребру A₁B₂,
2. Показываем, что отрезок MN перпендикулярен плоскости ABB₁.
3. Определяем линейный угол между плоскостями BMN и ABB₁ и вычисляем его.

Решение:

1. Выполняем чертеж к задаче.

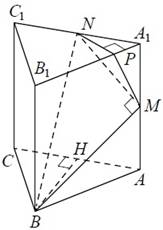
Призма правильная, следовательно, основанием ее является равносторонний треугольник. H делит AC пополам, поскольку в равностороннем треугольнике высота является биссектрисой и медианой.

2. Тогда высоту BH можно вычислить по теореме Пифагора из треугольника АВН:

3. Вычисляем длину BN² из треугольника BNH. Он тоже прямоугольный. По теореме Пифагора:

4. Отрезки BM и MN перпендикулярны, поскольку сумма квадратов их длин равна BN², то есть 63:

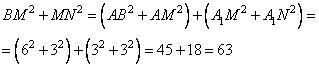
По теореме, обратной теореме Пифагора, BMN – прямоугольный, причем угол M прямой.

Первая часть задания выполнена: утверждение доказано.

б)

1. Проводим перпендикуляр NP к ребру A₁B₂.

Показываем , что NP перпендикулярна плоскости ABB₁. Из построения и условия (призма правильная) следует:

А это означает, что  .и прямая NP является проекцией MN на плоскость ABB₁.

3. Выше было доказано, что  . Тогда согласно теореме о трех перпендикулярах  . Их этого следует, что NMP – линейный угол искомого угла.

Вычисляем его.

N – середина отрезка A₁C₁, тогда NP = 1/2∙h, где h – высота в треугольнике A₁B₁C₁. А он равносторонний и равен треугольнику АВС. Следовательно,  , то есть  . По соотношениям в прямоугольном треугольнике.

 , откуда  .

Ответ: 

---

Второй вариант задания (из Ященко, № 1)

Алгоритм решения:

а)

1. Выполняем чертеж.
2. Устанавливаем подобие треугольников SAB и SMN.
3. Определяем вид сечения.

б)

1. Полагаем объем пирамиды равным V.
2. Определяем какую часть от всего объема пирамиды составляет каждая часть.
3. Находим отношение определенных объемов частей.
4. Записываем ответ.

Решение:

а)

1. Выполняем чертеж для задачи.

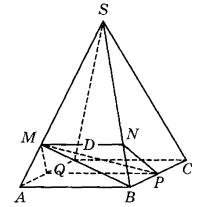
2. Пусть N — точка на ребре SB, причем SN:NB = 5:1. Треугольник SAB подобен треугольнику SMN, потому что в них две стороны пропорциональны и углы между ними равны.

3. Из подобия следует:  , сторона AB параллельна отрезку MN и  . PQ параллельна стороне АВ. Имеем: отрезки MN и PQ параллельны и не равны.

Рассмотрим треугольники MAQ и NBP. У них:

MA = NB, QA = PB

 . Значит, эти треугольники равны. А по свойству равных фигур MQ = NP. Тогда трапеция MNPQ является равнобедренной.

Отсюда следует, что сечение пирамиды плоскостью MPQ является трапецией MNPQ.

б)

1. Обозначаем объём пирамиды SABCD буквой V.

2. Многогранник AMQBNP составлен из пирамиды MABPQ (ее основание ABPQ) и пирамиды MBNP (ее с основание BNP).

Расстояния от точки М до (BNP) и от точки A до этой же плоскости равно 5:6, и S_BNP:S_SBC = 1:12.

3. Найдем отношение объёмов пирамид MBNP и ASBC: Оно равно 5:72. То есть объём V_MBNP = 5V|144.

S_ABPQ = ½ S_ABCD. Точка М отстоит от плоскости основания на расстоянии в 6 раз меньшем расстояния от вершины S до этого основании. Потому V_MABPQ = V|12.

Таким образом, V_AMQBNP = 5V|144+V|12=5V|144+12V|144=17V|144

Тогда отношение объёмов частей AMQBNP и CDSNPQM пирамиды равно

17:(144 – 17)127=17:127.

Ответ: 17 : 127.